Analisi matematica

In questa pagina si vuole agevolare la comprensione di alcuni concetti che rappresentano il cuore dell'analisi matematica semplicemente condensando e ricomponendo le spiegazioni contenute in un classico della materia. Whitehead ci presenta i concetti matematici rovesciando la prospettiva, partendo da presupposti diversi da quelli impiegati nei moderni manuali scolastici, in un modo a cui forse non siamo più abituati, ma che forse tra i tanti è quello più semplice.

Dire che nell’intorno di a la funzione (x) si avvicina a c con un grado di approssimazione k significa che si può trovare qualche intervallo che I) non comprenda a quale punto terminale e II) è tale che tutti i valori di f(x) ove x si trovi nell’intervallo e non sia a differiscono da c per meno di k. Per esempio, nell’intorno di 2, la funzione x² si avvicina a 4 con un grado di approssimazione di 0,5. Perché (1,9)²= 3,61 e (2,1)² = 4,41 e così l’intervallo richiesto da 1,9 a 2,1 che non contiene 2 quale punto terminale è stato trovato. Questo esempio mette in luce il fatto che quanto si afferma di una funzione f(x) nell’intorno di un numero a è distinto da quanto si afferma circa il valore di f(x) quando x = a; è necessario che ci sia un intervallo entro il quale l’affermazione sia vera. Così il semplice fatto che 2² = 4 non giustifica di per sé la nostra affermazione che nell’intorno di 2 la funzione x² è uguale a 4. Questa affermazione non sarebbe vera, perché non esiste nessun intervallo con la proprietà richiesta. Inoltre il fatto che 2² = 4 non giustifica di per se la nostra affermazione che nell’intorno di 2 la funzione x² si approssima a 4 con un gradi 0,5 anche se in realtà è stato dimostrato che questa affermazione è vera. Questo significa che, qualsiasi grado k si scelga, nell’intorno di a, f(x) si avvicina a f(a) con il grado di approssimazione k. Per esempio la funzione x² è continua per il valore 2 del suo argomento x, perché comunque venga scelto k, potremo sempre trovare un intervallo che I) contiene 2 non come punto terminale e II) sia tale che i valori x² per gli argomenti che si trovano entro di esso, si avvicinino a 4 cioè (2)² con un grado di approssimazione k. Così supponiamo di scegliere il grado di approssimazione 0,1; ora (1,999) = 3,996001; e (2,01)² = 4,0401; ed entrambi questi numeri differiscono da 4 per meno di 0,1. Perciò, entro l’intervallo da 1,999 a 2,01 i valori di ²  si avvicinano a 4 con il grado di approssimazione di 0,1. Egualmente, si può presentare un intervallo per qualsiasi altro grado di approssimazione si voglia provare. Una funzione f(x) è continua per un valore a del suo argomento, quando nell’intorno di a i suoi valori si avvicinano al suo valore in a entro qualsiasi grado di approssimazione; f(a) è il limite di f(x) in a per una funzione continua e per il valore di a considerato. Prendiamo l’esempio del treno. La sua velocità è continua quando supera la cabina segnalazioni se, per qualsiasi velocità si scelga di assegnargli (per esempio un milionesimo di miglio all’ora) esiste un intervallo di tempo che si estenda prima e dopo l’istante del passaggio, tale che in ogni momento entro tale intervallo la velocità del treno differisca da quella con la quale ha superato la cabina segnali per meno di un milionesimo di miglio all’ora;  e lo stesso sarà vero per qualsiasi altra velocità si indichi al posto di un milionesimo di miglio all’ora.

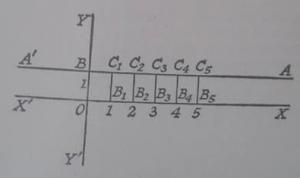
Ora, cosa si intende dicendo che il limite della funzione f(h) in a è l? il limite della funzione f(h) in a è una proprietà nell’intorno di a. In generale una funzione f(x) ha il limite l per un valore a del suo argomento x, quando nell’intorno di a i suoi valori si avvicinano ad l entro un qualsiasi grado di approssimazione. Comparando quest’ultima definizione con quella di continuità risulta evidente che una funzione è continua in a quando I) possiede un limite in a; e II) quel limite è eguale al suo valore in a. Nel caso del limite per un punto dove una funzione non è continua. Per esempio, prendiamo la funzione y = 1 il cui grafico è in figura. Questa presenta il valore 1 per tutti i valori dell’argomento x, tranne quando si tratti di numeri interi, cioè tranne che per x = 0, x = 1, x = 2, ecc., nel qual caso avrà valore 0. In un diagramma sarebbe la linea retta ABA’, tracciata parallela all’asse XOX’alla distanza di una unità di lunghezza da tale asse. Ma i punti B, C1, C2, C3, C4, ecc., che corrispondono ai valori 0, 1, 2, 3, 4, ecc. dell’argomento x debbono venire saltati, e al loro posto devono essere presi i punti 0, B1, B2, B3, B4 sull’asse OX. Pensiamo al limite di questa funzione quando x = 3. Notiamo che nella definizione di limite il valore della funzione in a (in questo caso a = 3) viene escluso.  Ma escludendo f(3)  i valori di f(x) quando x giace in un intervallo che I) contiene 3 non come estremo, e II) non si estende fino a 2 e a 4 sono tutti eguali a 1; e perciò questi valori si avvicinano a 1 entro qualsiasi grado di approssimazione. Quindi 1 è il limite di f(x) per il valore 3 dell’argomento x, ma per definizione f(3) = 0. Questo è un caso di funzione che possiede sia un valore che un limite per il valore 3 dell’argomento, ma il valore non è eguale al limite. Tornando alla funzione x²  per il valore 2 dell’argomento il suo valore è 2² cioè 4. Così, qui abbiamo una funzione con un valore e un limite che sono eguali. Ma il caso importante ai nostri fini è quello di una funzione che possiede un limite ma non un valore definito per un certo valore del suo argomento. Ad esempio 2x/x. Essa presenta la difficoltà che quando x è 0 2x/x è 0/0, e 0/0 e dunque il valore della funzione non hanno nessun significato ben definito. Ma per qualsiasi altro valore di x il valore della funzione 2x/x è 2, mentre non esiste un valore per x = 0. Egualmente, il limite di x²/x per x =a è a, qualsiasi sia a, cosicchè il limite di x²/x per x = 0 è 0. Ma il valore di x²/x per x = 0, prende la forma 0/0 che non ha un significato ben definito. Così la funzione x²/x ha un limite ma non ha nessun valore per 0. (Alfred North Whitehead)